On pose une suite d'ouverts denses dans \(O\) pour la topologie induite.

On les unie avec l'intérieur du complémentaire de \(O\) \(\to\) ça reste des ouverts.

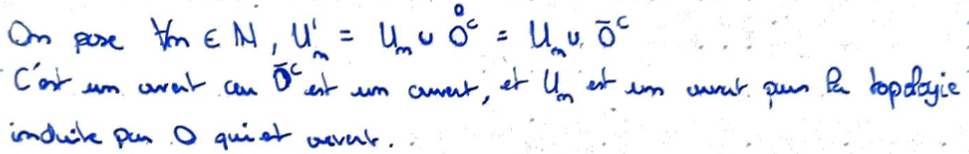
On montre que cette union est dense en montrant que leur intersection avec un ouvert de \(E\) est toujours non vide (par disjonction des cas).

Leur intersection est donc dense dans \(E\) d'après le Théorème de Baire.

En intersectant avec \(O\), on a la densité pour \(O\) puisque \(O\) et \(\overline O^C\) sont disjoint.

On pose une famille d'ouverts denses, leur intersection et un ouvert non vide.

Si on prend un point dans l'intersection de \(V\) et de \(U_0\), alors on a l'un de ses voisinages (car ouverts).

Par Compacité locale, on peut prendre un sous-voisinage compact.

Prendre l'Intérieur donne alors un ouvert non vide.

En itérant sur \(n\) et en construisant une suite décroissante de compacts, on a la densité.